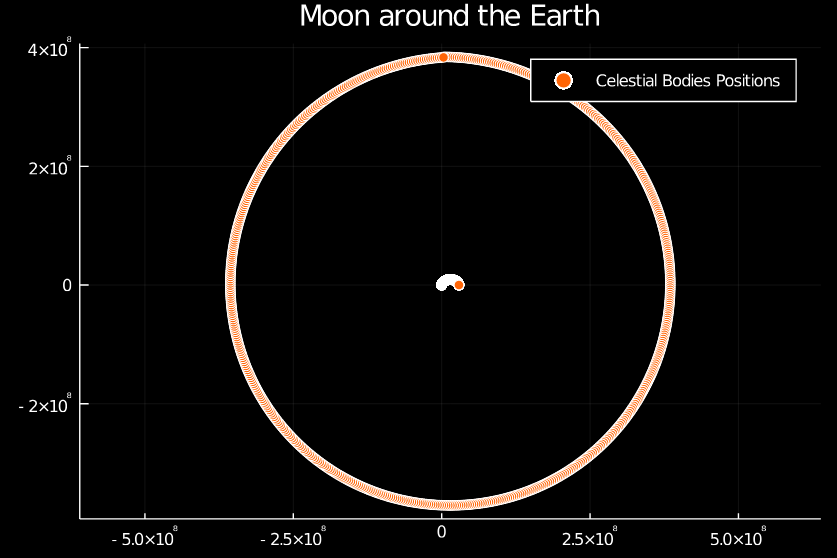
In this post we are going to do some basic astrophysics. We are going to simulate the movements of the Moon around the Earth using Julia.
Lets warm up with some imports:
using JLD
using Plots
using LinearAlgebra
Now we will write two functions, one that given an array of all positions, velocities and masses returns the velocities at that point, so, trivially:
velocities(p, v, m) = v
and another which calculates the acceleration given the same inputs. For that we will need to iterate through all point masses and calculate the acceleration between those bodies, summing everything for each body.
function accelerations(p, v, m)
local bodies = length(p)
map(function (i)
local sum = [0; 0]
for j in 1:bodies
if i != j
local d = p[j]-p[i]
sum += normalize(d)*(6.67408e-11*m[j]/norm(d)^2)
end
end
sum
end, 1:bodies)
end
Do notice the gravitational constant tucked in there!
Now we create our integrator, in this case the RK4 integrator:
function integrate_rk4(p, v, m, Δt::Real)
kp₁ = velocities(p, v, m)
kv₁ = accelerations(p, v, m)
kp₂ = velocities(p + kp₁*Δt/2, v + kv₁*Δt/2, m)
kv₂ = accelerations(p + kp₁*Δt/2, v + kv₁*Δt/2, m)
kp₃ = velocities(p + kp₂*Δt/2, v + kv₂*Δt/2, m)
kv₃ = accelerations(p + kp₂*Δt/2, v + kv₂*Δt/2, m)
kp₄ = velocities(p + kp₃*Δt, v + kv₃*Δt, m)
kv₄ = accelerations(p + kp₃*Δt, v + kv₃*Δt, m)
p+Δt/6*(kp₁+2*kp₂+2*kp₃+kp₄), v+Δt/6*(kv₁+2*kv₂+2*kv₃+kv₄), m
end
Notice how each step uses the values from the previous step. Finally, lets define the initial masses, positions and velocities
# Earth at origin
p = [ [0; 0], [0; 384402e3 ] ]
# Earth still
v = [ [0; 0], [1.022e3; 0] ]
# Masses
m = [ 5.972e24 , 7.348e22 ]
Finally, lets just call our integrator over and over, with time step of one hour, for 26.8 days, which is the time the Moon takes for one full revolution around the Earth.
orbits_x = []
orbits_y = []
for t ∈ 1:24*26.8
global p, v, m, orbits_x, orbits_y
p, v, m = integrate_rk4(p, v, m, 3600)
for i ∈ 1:length(p)
push!(orbits_x, p[i][1])
push!(orbits_y, p[i][2])
end
end
plot(
orbits_x,
orbits_y,
seriestype = :scatter,
title = "Moon around the Earth",
label = "Celestial Bodies Positions",
aspect_ratio=:equal
)
And behold, we have simulated, with physically accurate constants, the movements of the moon: